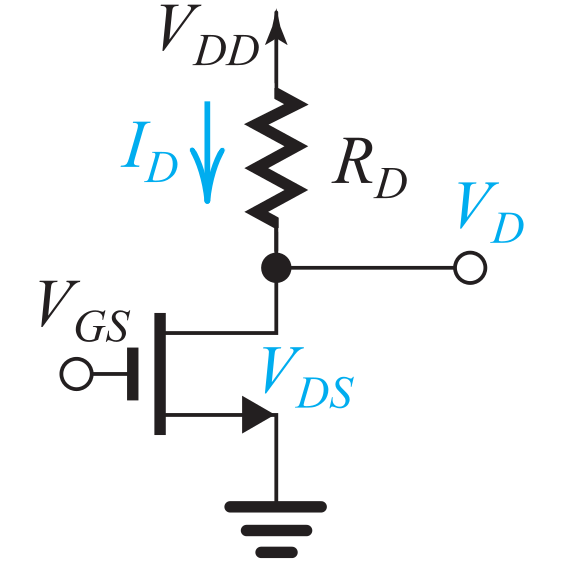
EE315Thumbnail EE 315 Introduction to Electronic Analysis & Design: This course highlights the properties of diode, bipolar transistors, FET and operational amplifiers, analysis of DC and AC small-signal operation and circuit models for the design and analysis of electronic circuits. Prerequisite: EE 213 (Electric Circuit Analysis I)
EE316Thumbnail EE 316 Electric Circuits & Electronic Design Lab: This hands-on laboratory course covers electric circuit experiments including first and second order DC circuits, maximum power transfer, impedance measurements, transformers, measurement of electronic device characteristics, and design and testing of operational amplifier circuits and single-stage amplifiers using MOSFETs and BJTs. Pre/co-requisite: EE 315 (Introduction to Electronic Analysis & Design).
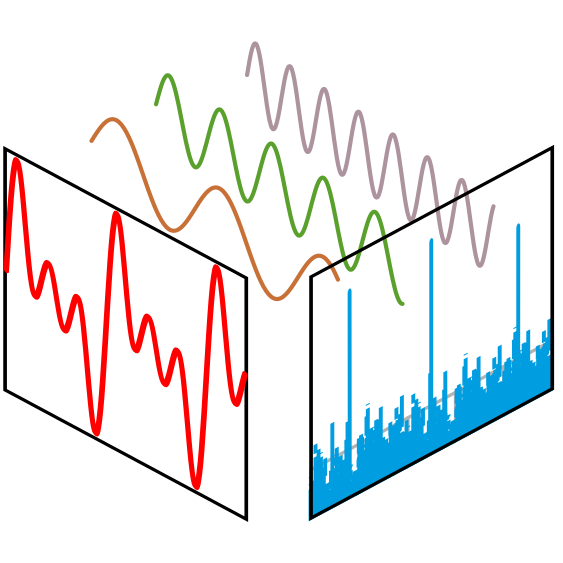
EE382Thumbnail EE 382 Analytic Methods of Continuous Time Signals & Systems: This course focuses on Fourier Series, Fourier and Laplace transforms with emphasis on their physical interpretation. System representation by transfer functions and impulse response functions, convolution integral, transient response, and modeling and simulation. Prerequisites: EE 213 (Electric Circuit Analysis I), MA 238 (Applied Differential Equations), and MA 244 (Introduction to Linear Algebra).
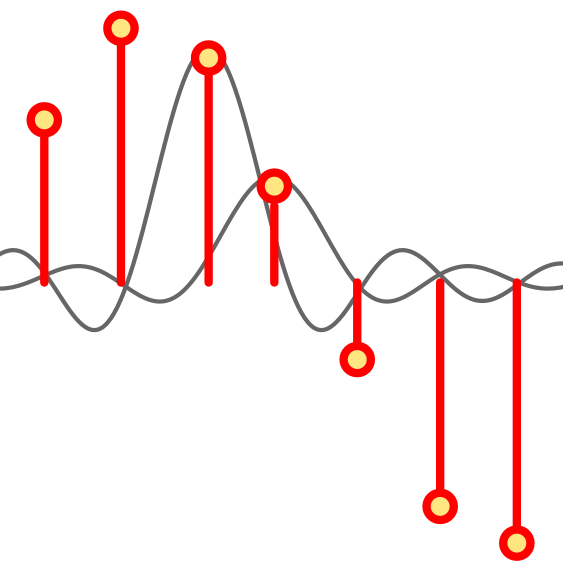
EE383Thumbnail EE 383 Analytic Methods of Discrete Time & Multivariable Signals & Systems: This course highlights discrete time signals and systems, sampling techniques, Z and discrete Fourier transforms, multivariable systems. An introduction to digital signal processingis also given. Prerequisite: EE 382 (Analytic Methods of Continuous Time Signals & Systems).
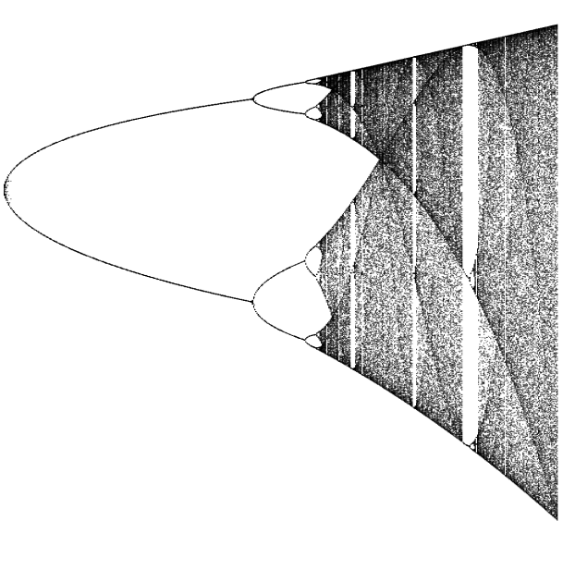
EE518Thumbnail EE 418/518 Nonlinear Dynamics & Chaos: This course provides students with an introduction nonlinear dynamics and chaos. Topics will address system stability, linearization, equilibrium/steady-state solutions, bifurcations, periodic solutions, limit cycles, oscillators, chaos, iterated maps and chaos control/synchronization. Various tools and methods used for analysis and design of nonlinear circuits and systems will be covered. When possible, systems will be treated analytically, however, general treatment of systems using numerical methods will be shown with MATLAB and/or Python. Ultimately, this course will provide experience for students beyond the limited behavior of low-degree linear circuits and systems towards complex behaviors where determinism doesn’t always imply predictability.
EE525Thumbnail EE 425/525 Fundamentals of Radar Systems: This course provides students with an introduction to radar systems and basic radar analysis. Common radar topologies and construction methods are provided. Particular focus on analysis of the radar range equation and its various terms is given. The radar range equation allows characterization of the energy found in transmitted/received signals and a corresponding noisy environment. This fundamental equation is key for all aspects of radar design and analysis including peak and average power, directive gain of antennas, target characteristics, operating frequencies, waveform properties, noise and loss factors. The information in this course describes transmission, reception and processing in radar systems even when the signals of interest are embedded in noise.
EE510OpenICThumbnail EE 410/510 Open-source Integrated Circuit Design: Coming soon…
APAEPScienceThumbnail APAEP Conceptual Integrated Science: Coming soon…

Teaching Philosophy:

Teaching Statement: I love to learn. I especially love to learn with others through collaboration, rigor and playful interpretation. My courses often boot-strap from practical observations and build toward challenges that engage students to think beyond traditional boundaries.

Summary: As an educator, my primary goal is to focus on student growth towards the high standards of university-level institutions. This takes work – reinforcing fundamentals and sharing a wonder for the material. I hope to create an environment that illustrates how to delight in this work. Engineering concepts are amazing. Topics often interconnect and deepen one another. Engineering turns the most satisfying results from mathematics and physics into the art of what is possible. If students earn these tools, they are empowered to build and analyze in new, better ways. For example, some students connect with the beauty of using an impulse response to turn a linear, time-invariant, differential equation problem into a convolution problem. Other students simply dislike differential equations to the point that any other alternative feels like a miracle. Both groups are empowered by solving LTI systems for an arbitrary input.

How do you get students to buy into this? I’m still learning. I try to seed an attitude and hope that is reflected. I try to give an example through my behavior. In my experience, generally, students tend to learn best by example. This tendency seems to hold not only for material in the classroom but also for developing excitement for learning, discipline for rigor, creativity for research and temperament for teamwork & mentorship.

However, sometimes I have more selfish goals if I’m being honest. Courses with roots showing subtle implications of fundamentals or sometimes slippery concepts give me longing. I think this is shared by Leonard Susskind. He states during an online lecture in Stanford’s Statistical Mechanics offering, “The reason I teach it (stat. mech.) is not for you, its for me. I love teaching it. My life consists of learning and forgetting and learning and forgetting statistical mechanics.”

Dr. Susskind’s comment is in line with a concept that has been shared with me many times – education is what is left when someone forgets what they have learned. In short, I see great value in how much I learn when teaching and each time around I hope to forget a little less while making new observations. As Georgia O’Keeffe painted the slightly different perspective of her same patio door more than 20 individual times, I hope to appreciate the perspectives of my courses as I repeat and relearn the material throughout my career.

I am still growing as an educator. I value feedback and self-reflection to progress my teaching philosophy. Each time I update my teaching statement, I feel a bit embarrassed at what was written before. I interpret this as evidence of my growth. My outlook is influenced by many great teachers and mentors. They have shown me examples of patience, compassion, rigor, curiosity, work-life balance and style. My mentors have been so generous. It took time to realize the monumental energy associated with their level of composure and openhandedness. Currently, my job is to find that energy on demand as needed by my students.